Proper length
In relativistic physics, proper length is an invariant measure of the distance between two spacelike-separated events, or of the length of a spacelike path within a spacetime.
The measurement of lengths is more complicated in the theory of relativity than in classical mechanics. In classical mechanics, lengths are measured based on the assumption that the locations of all points involved are measured simultaneously. But in the theory of relativity, the notion of simultaneity is dependent on the observer. Proper lengths provide an invariant measure, whose value is the same for all observers.
Proper length is analogous to proper time. The difference is that proper length is the invariant interval of a spacelike path or pair of spacelike-separated events, while proper time is the invariant interval of a timelike path or pair of timelike-separated events.
Proper length between two events
In special relativity, the proper length between two spacelike-separated events is the distance between the two events, as measured in an inertial frame of reference in which the events are simultaneous. So if the two events occur at opposite ends of an object, the proper length of the object is the length of the object as measured by an observer which is at rest relative to the object.
In any inertial frame of reference, the proper length L is
,
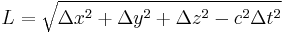where
- Δt is the difference in the temporal coordinates of the two events,
- Δx, Δy, and Δz are differences in the linear, orthogonal, spatial coordinates of the two events, and
- c is the speed of light.
Two events are spacelike-separated if and only if the above formula gives a real, non-zero value for L.
Proper length of a path
The above formula for the proper length between two events assumes that the spacetime in which the two events occur is flat. Hence, the above formula cannot in general be used in general relativity, in which curved spacetimes are considered. It is, however, possible to define the proper length of a path in any spacetime, curved or flat. In a flat spacetime, the proper length between two events is the proper length of a straight path between the two events. In a curved spacetime, there may be more than one straight path (geodesic) between two events, so the proper length of a straight path between two events would not uniquely define the proper length between the two events.
Along an arbitrary spacelike path P, the proper length is given in tensor syntax by the line integral
,
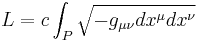where
- gμν is the metric tensor for the current spacetime and coordinate mapping, and
- dxμ is the coordinate separation between neighboring events along the path P.
In the equation above, the metric tensor is assumed to use the +--- metric signature, and is assumed to be normalized to return a time instead of a distance. The - sign in the equation should be dropped with a metric tensor that instead uses the -+++ metric signature. Also, the 
should be dropped with a metric tensor that is normalized to use a distance, or that uses geometrized units.